
DFS(Depth-First Search)는 그래프나 트리에서 널리 사용되는 탐색 알고리즘으로, 시작 정점에서 한 경로를 끝까지 탐색한 후에 다른 경로로 이동하는 방식으로 동작합니다. 모든 경로를 탐색하거나 특정 경로를 찾는 데 유용하며, 다양한 문제 해결에 활용됩니다.
1. DFS의 개념
DFS는 스택(Stack) 자료구조를 기반으로 하거나 재귀를 사용하여 구현되며, 그래프의 한 경로를 깊게 탐색한 후, 더 이상 탐색할 노드가 없을 때 이전 경로로 되돌아갑니다. 이를 "백트래킹(Backtracking)"이라고 합니다.
(일반적으로 코딩테스트 문제 풀이 시 재귀로 dfs를 구현합니다.)
2. DFS의 동작 원리
- 시작 정점을 방문하고 스택 또는 재귀 호출을 통해 탐색합니다.
- 현재 정점의 인접 정점 중 방문하지 않은 정점을 선택하여 이동합니다.
- 더 이상 방문할 인접 정점이 없으면 이전 정점으로 되돌아갑니다.
- 그래프의 모든 정점을 방문할 때까지 이 과정을 반복합니다.
동작 구조도
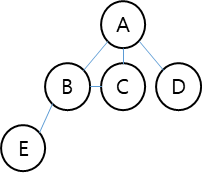
다음은 DFS의 동작 과정을 시각적으로 표현한 구조도입니다.
시작 정점: A
1단계: 스택=[A]
A 방문 → 인접 정점 B, C, D 중 B 선택
방문 순서: A → B
2단계: 스택=[A, B]
B 방문 → 인접 정점 E 선택
방문 순서: A → B → E
3단계: 스택=[A, B, E]
E 방문 → 되돌아감 (더 이상 인접 정점 없음)
4단계: 스택=[A, B]
C 방문
방문 순서: A → B → E → CDFS는 한 경로를 끝까지 깊게 들어가면서 탐색하고 다시 되돌아오는 방식으로 작동합니다.
3. DFS의 시간 복잡도
- 시간 복잡도: O(V + E)
- V: 정점(Vertex)의 수
- E: 간선(Edge)의 수
- 각 정점을 한 번씩 방문하고, 모든 간선을 확인하기 때문입니다.
- 공간 복잡도: O(V)
- 재귀 호출 스택 또는 명시적 스택의 크기에 따라 공간이 필요합니다.
4. DFS 구현 예시 코드(재귀 방식)
C 언어 구현
#include <stdio.h>
#include <stdbool.h>
#define MAX 100
int graph[MAX][MAX];
bool visited[MAX];
void dfs(int v, int n) {
visited[v] = true;
printf("%d ", v);
for (int i = 0; i < n; i++) {
if (graph[v][i] == 1 && !visited[i]) {
dfs(i, n);
}
}
}
int main() {
int n = 6;
graph[0][1] = graph[0][2] = 1;
graph[1][3] = graph[1][4] = 1;
graph[2][5] = 1;
dfs(0, n);
return 0;
}Java 구현
import java.util.*;
public class DFS {
public static void main(String[] args) {
int n = 6;
List<List<Integer>> graph = new ArrayList<>();
for (int i = 0; i < n; i++) {
graph.add(new ArrayList<>());
}
graph.get(0).add(1);
graph.get(0).add(2);
graph.get(1).add(3);
graph.get(1).add(4);
graph.get(2).add(5);
boolean[] visited = new boolean[n];
dfs(graph, 0, visited);
}
public static void dfs(List<List<Integer>> graph, int v, boolean[] visited) {
visited[v] = true;
System.out.print(v + " ");
for (int neighbor : graph.get(v)) {
if (!visited[neighbor]) {
dfs(graph, neighbor, visited);
}
}
}
}Python 구현
def dfs(graph, v, visited):
visited.add(v)
print(v, end=' ')
for neighbor in graph[v]:
if neighbor not in visited:
dfs(graph, neighbor, visited)
# 그래프 예시
graph = {
0: [1, 2],
1: [3, 4],
2: [5],
3: [],
4: [],
5: []
}
visited = set()
dfs(graph, 0, visited)5. DFS의 장단점
장점
- 메모리 효율성: 그래프가 넓은 경우(BFS와 비교했을 때) 상대적으로 메모리를 적게 사용합니다.
- 백트래킹 문제 해결: 경로를 끝까지 탐색하므로 백트래킹 문제에 유용합니다.
단점
- 무한 루프 가능성: 순환 그래프에서 방문 여부를 확인하지 않으면 무한 루프에 빠질 수 있습니다.
- 최단 경로 보장 불가: DFS는 최단 경로를 보장하지 않습니다.
같이 보면 좋은 글
1) DFS, BFS 비교
2024.12.19 - [알고리즘] - DFS(깊이 우선 탐색)와 BFS(너비 우선 탐색) 알고리즘 비교(차이점, 장단점, 예시코드, 활용도)
DFS(깊이 우선 탐색)와 BFS(너비 우선 탐색) 알고리즘 비교(차이점, 장단점, 예시코드, 활용도)
2024.12.19 - [알고리즘] - DFS (깊이 우선 탐색, Depth-First Search) 알고리즘 - C언어, Java, Python 예시코드, 시간복잡도 DFS (깊이 우선 탐색, Depth-First Search) 알고리즘 - C언어, Java, Python 예시코드, 시간복잡
best-coding.tistory.com
2) DFS, 백트래킹, 브루트포스 비교
2024.12.20 - [알고리즘] - 브루트포스, DFS, 백트래킹 차이점 정리
브루트포스, DFS, 백트래킹 차이점 정리
브루트포스(Brute Force), DFS(깊이 우선 탐색), 백트래킹(Backtracking)은 알고리즘 문제 해결에서 자주 언급되는 기법입니다. 이 세 가지는 개념적으로 유사한 점이 많지만, 실제 사용 방식과 효율성에
best-coding.tistory.com
3) 메모이제이션 적용을 통해 DFS 성능 개선하기
2024.12.21 - [알고리즘] - 메모이제이션을 통한 성능개선 (3) - DFS
메모이제이션을 통한 성능개선 (3) - DFS
DFS(Depth First Search)는 그래프 탐색 및 다양한 문제를 해결하는 데 널리 사용되는 알고리즘입니다. 이 알고리즘에 메모이제이션(Memoization)을 활용하면 중복 계산을 제거하고 효율성을 극대화할 수
best-coding.tistory.com
'알고리즘' 카테고리의 다른 글
| 버킷(Bucket) 알고리즘 - 코딩테스트에서 시간을 단축하는 비법(시간복잡도, C언어,Java,Python 예시코드) (0) | 2024.12.20 |
|---|---|
| 이진 탐색(Binary Search) 알고리즘 - C언어, Java, Python 예시코드, UpperBound, LowerBound (2) | 2024.12.19 |
| 그리디 알고리즘 (Greedy Algorithm) (1) | 2024.12.19 |
| DFS(깊이 우선 탐색)와 BFS(너비 우선 탐색) 알고리즘 비교(차이점, 장단점, 예시코드, 활용도) (0) | 2024.12.19 |
| BFS(너비 우선 탐색, Breadth-First Search) 알고리즘 - C언어, Java, Python 예시코드 포함, 시간복잡도 (0) | 2024.12.19 |




댓글